MimIR 0.1
MimIR is my Intermediate Representation
Loading...
Searching...
No Matches
The math Plugin

Table of Contents

See also
mim::plug::math

Introduces a type constructor %math.F for viarious IEEE-754 floating-point formats and a set of operations to calculate with instances of these types. All operations with the exception of %math.conv expect a Nat just in front of its actual argument. Here you can fine adjust via mim::plug::math::Mode how strictly you want to obey floating-point transformations.

Types

%math.F

A floating-point type with p many bits as precision and e many bits as exponent. The sign bit is neither included in p nor in e. Thus, the total number of bits occupied by a value of this type is p + e + 1.

axm %math.F: «2; Nat» → *;
let %math.f16 = (10, 5);
let %math.f32 = (23, 8);
let %math.f64 = (52, 11);
let %math.bf16 = ( 7, 8);
let %math.nvtf32 = (10, 8);
let %math.amdfp24 = (16, 7);
let %math.pxr24 = (15, 8);
let %math.F16 = %math.F %math.f16;
let %math.F32 = %math.F %math.f32;
let %math.F64 = %math.F %math.f64;
let %math.BF16 = %math.F %math.bf16;
let %math.NVTF32 = %math.F %math.nvtf32; // actually 19 bits; aligns to 32 bit
let %math.AMDFP24 = %math.F %math.amdfp24;
let %math.PXR24 = %math.F %math.pxr24;

Numerical Operations

%math.arith

Arithmetic operations.

axm %math.arith(add, sub, mul, div, rem):
{pe: «2; Nat»} → Nat → «2; %math.F pe» → %math.F pe, normalize_arith;
lam %math.minus {pe: «2; Nat»} (m: Nat) (a: %math.F pe): %math.F pe =
%math.arith.sub m (0:(%math.F pe), a);

%math.extrema

Minimum and Maximum.

  • min or Max

  • i: Follows the behavior of libm’s fmin/fmax.

    If either operand is a NaN, returns the other non-NaN operand. Returns NaN only if both operands are NaN. The returned NaN is always quiet. If the operands compare equal, returns a value that compares equal to both operands. This means that fmin(+/-0.0, +/-0.0) could return either -0.0 or 0.0.

  • I: Follows the semantics of minNum/maxNum specified in the draft of IEEE 754-2018.

    If either operand is a NaN, returns NaN. Otherwise returns the lesser of the two arguments. -0.0 is considered to be less than +0.0 for this intrinsic.

Subtag Alias N M
im fmin o o
iM fmax o x
Im ieee754min x o
IM ieee754max x x
axm %math.extrema(im = fmin, iM = fmax,
Im = ieee754min, IM = ieee754max):
{pe: «2; Nat»} → Nat → «2; %math.F pe» → %math.F pe, normalize_extrema;

%math.tri

Trigonometric and hypberbolic functions.

  • FF: sine, cosine, tangent, unused
  • Hyperbolic counterpart
  • Arcus/Area counterpart (inverse)
Subtag Alias A H R FF Meaning Semantics
ahff sin o o o oo sine $\sin x$
ahfF cos o o o xo cosine $\cos x$
ahFf tan o o o ox tangent $\tan x$
ahFF o o o xx unused -
aHff sinh, h o x o oo hyperbolic sine $\sinh x$
aHfF cosh o x o xo hyperbolic cosine $\cosh x$
aHFf tanh o x o ox hyperbolic tangent $\tanh x$
aHFF o x o xx unused -
Ahff asin , a x o o oo arcus sine $\textrm{asin}\,x$
AhfF acos x o o xo arcus cosine $\textrm{acos}\,x$
AhFf atan x o o ox arcus tangent $\textrm{atan}\,x$
AhFF x o o xx arcus unused -
AHff asinh x x o oo area hyperbolic sine $\textrm{asinh}\,x$
AHfF acosh x x o xo area hyperbolic cosine $\textrm{acosh}\,x$
AHFf atanh x x o ox area hyperbolic tangent $\textrm{atanh}\,x$
AHFF x x o xx unused -
axm %math.tri(ahff = sin , ahfF = cos , ahFf = tan , ahFF,
aHff = sinh = h, aHfF = cosh, aHFf = tanh, aHFF,
Ahff = asin = a, AhfF = acos , AhFf = atan , AhFF,
AHff = asinh , AHfF = acosh, AHFf = atanh, AHFF):
{pe: «2; Nat»} → Nat → %math.F pe → %math.F pe, normalize_tri;

%math.pow

Power function: 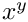$x^y$

axm %math.pow: {pe: «2; Nat»} → Nat → «2; %math.F pe» → %math.F pe, normalize_pow;

%math.rt

Square and cube root:

Name Meaning Semantics
%math.rt.sq square root $\sqrt{x}$
%math.rt.cb cube root $\sqrt[3]{x}$
axm %math.rt(sq, cb): {pe: «2; Nat»} → Nat → %math.F pe → %math.F pe, normalize_rt;

%math.exp

Exponential function and logarithm:

  • Logarithm
  • BB: natural, binary, decimal, unused
Subtag Alias L BB Meaning Semantics
lbb exp o oo natural exponential $e^x$
lbB exp2, bin o ox exponential with base 2 $2^x$
lBb exp10, dec o xo exponential with base 10 $10^x$
lBB unused o xx - unused
Lbb log x oo natural logarithm $\ln x$
LbB log2 x ox logarithm with base 2 $\log_2 x$
LBb log10 x xo logarithm with base 10 $\log_{10} x$
LBB unused x xx - unused
axm %math.exp(lbb = exp, lbB = exp2 = bin, lBb = exp10 = dec, lBB,
Lbb = log, LbB = log2 , LBb = log10 , LBB):
{pe: «2; Nat»} → Nat → %math.F pe → %math.F pe, normalize_exp;

%math.er

Error and complementary error function.

Name Meaning Semantics
%math.er.f error function $\frac{2}{\sqrt\pi}\int_0^x e^{-t^2}\,dt$
%math.er.fc complementary error function $\frac{2}{\sqrt\pi}\int_x^\infty e^{-t^2}\,dt = 1 - \textrm{erf}(x)$
axm %math.er(f, fc): {pe: «2; Nat»} → Nat → %math.F pe → %math.F pe, normalize_er;

%math.gamma

Gamma function and its natural logarithm.

Name Meaning Semantics
%math.gamma.t gamma function $\Gamma(x) = \int_0^\infty t^{x-1} e^{-t}\,dt$
%math.gamma.l natural logarithm of gamma function $\ln \mid \int_0^\infty t^{x-1} e^{-t}\,dt \mid$
axm %math.gamma(t, l): {pe: «2; Nat»} → Nat → %math.F pe → %math.F pe, normalize_gamma;

%math.abs

Absolute value of a floating point number

axm %math.abs: {pe: «2; Nat»} → Nat → %math.F pe → %math.F pe, normalize_abs;

%math.round

Common rounding operations for floating points:

  • floor
  • ceil
  • round
  • truncate
Name Meaning Semantics
%math.round.f round down $\lfloor x \rfloor $
%math.round.c round up $\lceil x \rceil $
%math.round.r round to nearest integer $round (x)$
%math.round.t round towards zero $trunc (x)$
axm %math.round(f,c,r,t): {pe: «2; Nat»} → Nat → %math.F pe → %math.F pe, normalize_round;

Other Operations

%math.cmp

Floating point comparison is made of 4 disjoint relations:

  • Unordered (yields true if either operand is a QNAN)
  • Greater
  • Less
  • Equal
Subtag Alias U G L E Meaning
ugle f o o o o always false
uglE e o o o x ordered and equal
ugLe l o o x o ordered and less
ugLE le o o x x ordered and less or equal
uGle g o x o o ordered and greater
uGlE ge o x o x ordered and greater or equal
uGLe ne o x x o ordered and not equal
uGLE o o x x x ordered (no NaNs)
Ugle u x o o o unordered (either NaNs)
UglE ue x o o x unordered or equal
UgLe ul x o x o unordered or less
UgLE ule x o x x unordered or less or equal
UGle ug x x o o unordered or greater
UGlE uge x x o x unordered or greater or equa
UGLe une x x x o unordered or not equal
UGLE t x x x x always true
axm %math.cmp(ugle = f, uglE = e, ugLe = l, ugLE = le,
uGle = g, uGlE = ge, uGLe = ne, uGLE = o,
Ugle = u, UglE = ue, UgLe = ul, UgLE = ule,
UGle = ug, UGlE = uge, UGLe = une, UGLE = t):
{pe: «2; Nat»} → Nat → «2; %math.F pe» → Bool, normalize_cmp;

%math.conv

Conversion between floating point and index types - both signed and unsigned - of different sizes.

axm %math.conv(s2f, u2f): { ss: Nat } → [dpe: «2; Nat»] → Idx ss → %math.F dpe, normalize_conv;
axm %math.conv(f2s, f2u): {spe: «2; Nat»} → [ ds: Nat ] → %math.F spe → Idx ds, normalize_conv;
axm %math.conv(f2f): {spe: «2; Nat»} → [dpe: «2; Nat»] → %math.F spe → %math.F dpe, normalize_conv;

%math.slf

Standard logistic function of a floating point number ( 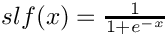$slf(x) = \frac{1}{1+e^{-x}}$)

lam %math.slf {pe : <<2; Nat>>} (m : Nat) (x : %math.F pe): %math.F pe =
%math.arith.div m ((%math.conv.f2f pe 1.0:(%math.F64)), %math.arith.add m ((%math.conv.f2f pe 1.0:(%math.F64)), %math.exp.exp m (%math.minus m x)));

%math.sgn

Sign function

lam %math.sgn {pe : <<2; Nat>>} (m : Nat) (x : %math.F pe): %math.F pe =
((%math.conv.f2f pe -1.0:(%math.F64)), ((%math.conv.f2f pe 0.0:(%math.F64)), (%math.conv.f2f pe 1.0:(%math.F64)))#(%math.cmp.g m (x,(%math.conv.f2f pe 0.0:(%math.F64)))))#(%math.cmp.ge m (x, (%math.conv.f2f pe 0.0:(%math.F64))));

%math.rrt

Reciprocal of the square root ( $rrt(x) = \frac{1}{\sqrt{x}}$)

lam %math.rrt {pe : <<2; Nat>>} (m : Nat) (x : %math.F pe): %math.F pe =
%math.arith.div m (%math.conv.f2f pe 1.0:(%math.F64), %math.rt.sq m x);